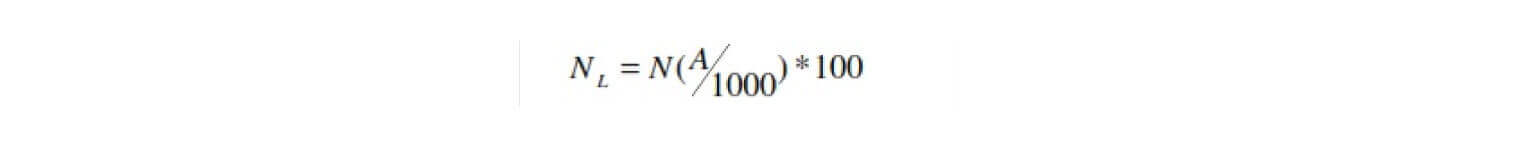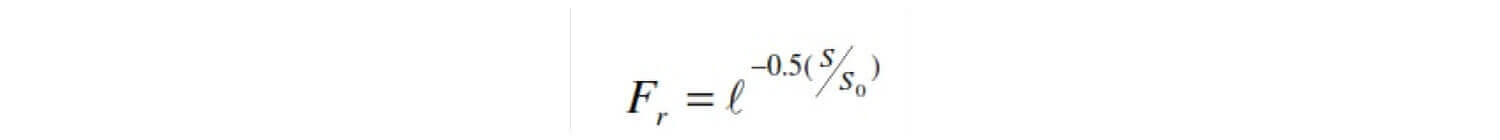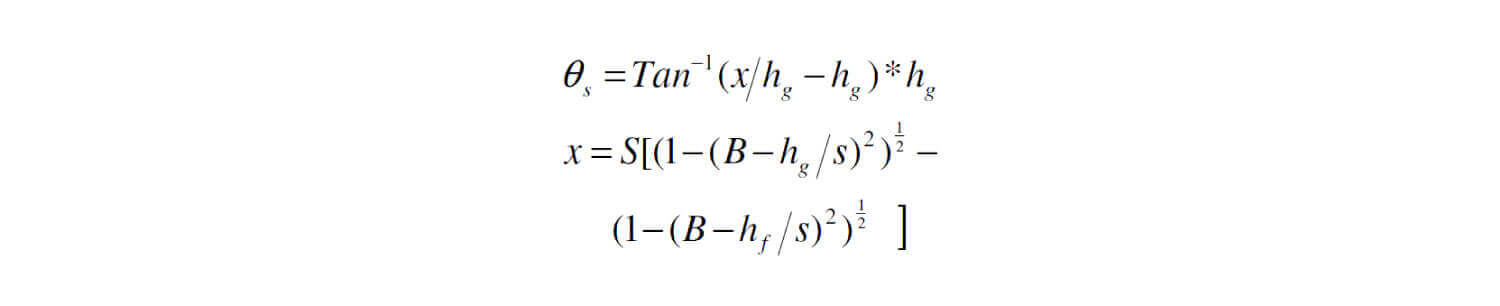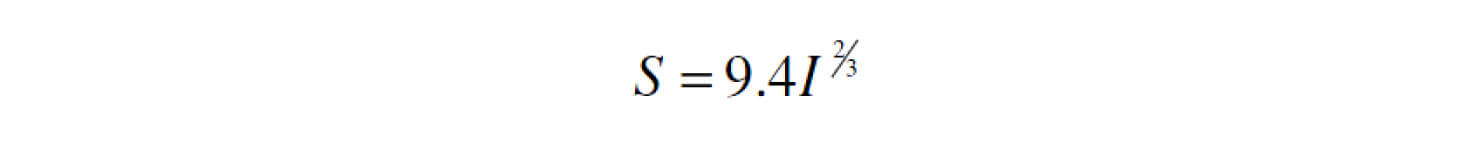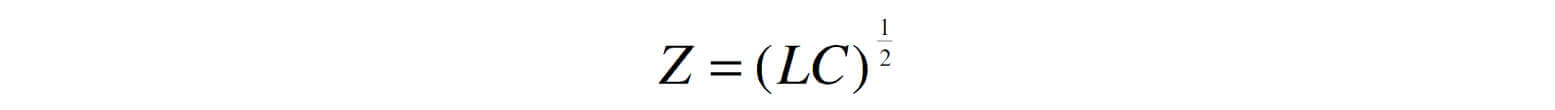Introducción
Hacia la mitad del siglo XVIII Benjamín Franklin demostró por primera vez la naturaleza eléctrica del rayo. Elevando una cometa en medio de una tormenta eléctrica y conduciendo una descarga hasta un condensador (botella de Leyden), demostró que había almacenado algo que presentaba el mismo comportamiento que las cargas eléctricas (que se generaban en esa época por fricción). Simultáneamente en otros lugares del mundo se realizaban investigaciones similares como la del científico ruso Giorgi W. Richman, quien pereció electrocutado en una de sus pruebas.
Más tarde, el mismo B. Franklin inventaría el pararrayos, para defender las edificaciones y personas de los efectos del rayo.
Cuando a principios del siglo XX, aparecieron las primeras líneas de transmisión, volvió el rayo a causar problemas que representaban grandes perjuicios al transporte de energía eléctrica; desde entonces comienzan proyectos de investigación de gran magnitud.
En 1905 se reportan ya estudios fotográficos de descargas atmosféricas realizadas con una cámara móvil [1]. Vienen luego proyectos donde se miden gradientes causados por la carga de las nubes [2], se utilizan el klidonógrafo [3], el oscilógrafo [4] y muchos otros medios para un estudio detallado de la descarga atmosférica y su efecto en los sistemas de potencia eléctrica.
Con la construcción en los años veinte de las primeras líneas a 220 kV, se empieza a considerar importante la realización de mapas isoceráunicos, se van perfeccionando cada vez más las metodologías de recolección y procesamiento de datos de salidas de las líneas y se va adquiriendo una buena comprensión del efecto de las descargas atmosféricas sobre las líneas.
Sin embargo, hoy se hace necesario emprender proyectos que eviten el alto número de salidas en algunas líneas y elaborar un diseño más apropiado de líneas futuras, para evitar tanto exceder un número establecido de salidas, como también, el sobredimensionamiento que se hace evidente en un número de aisladores exagerado.
1.0 Características de las descargas atmosféricas
1.1 Formación y evolución de la descarga
1.1.1 Carga eléctrica en las nubes
Las descargas atmosféricas se presentan cuando se forman grandes concentraciones de carga eléctrica en las capas de la atmósfera inmediatamente inferiores a la estratosfera (alturas entre 5 y 12Km). Al aumentar la carga se forman potenciales de hasta 300 MV entre nubes y tierra.
La descarga se forma en nubes de tormenta del tipo cumulonimbus. Estas se caracterizan por estar formadas por columnas de aire caliente que ascienden por convección, cuando la atmósfera se hace inestable, debido a grandes gradientes de temperatura. El interior de esas nubes, es recorrido por rápidas corrientes de aire ascendentes y descendentes de velocidades hasta de 300km.
La carga eléctrica se forma al separar estas fuertes corrientes de aire, las partículas de agua y hielo en partículas ionizadas. La carga se concentra en un disco de un diámetro de 10 Km. y una altura aproximada de 5 km. Esta carga es en la mayoría de los casos predominantemente negativa.
A medida que se empieza a incrementar la carga y el voltaje en las cercanías de las nubes cargadas, se empieza a rebasar el gradiente crítico, (30 kV en aire seco,
10 kV en las condiciones de presión y presencia de gotas de agua existentes en las nubes). Se empieza a presentar ionización del aire y por lo tanto, se van formando caminos para la conducción de la carga hacia el punto de potencial cero que es la tierra.
1.1.2 Evolución de la descarga
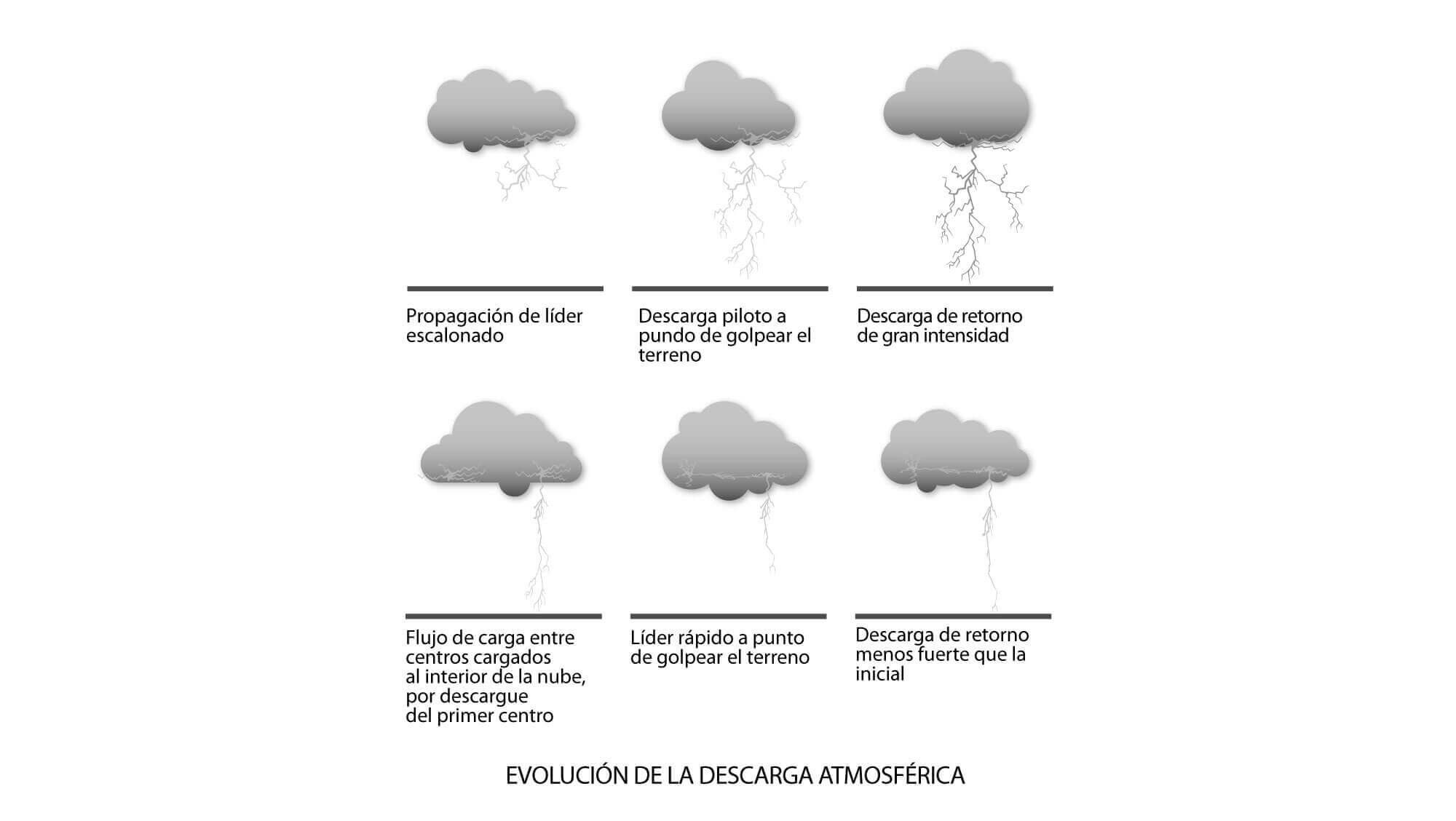
El camino de ionización que se inicia, lleva un primer flujo de carga hacia capas más bajas. Este primer flujo es llamado el líder. El líder desciende unos 50 a 100m en un microsegundo, detiene su marcha unos 50 microsegundos mientras se acumula la carga transferida desde la nube y se forma un nuevo camino ionizado que va a crear un nuevo avance del líder (figura 1). Estos avances y reposos de este primer flujo de carga, hacen que se le conozca como el líder escalonado. Este sigue avanzando hasta llegar cerca de los objetos y estructuras más altos, los cuales empiezan a emitir chispas que van al encuentro del líder.
Al cerrarse eléctricamente el camino a tierra, la carga se desplaza a una velocidad vertiginosa, produciéndose la descarga de retorno de gran luminosidad, etapa del rayo considerada como la más energética de todas.
Luego, con intervalos de 0.01 a 0.1 segundos se producen nuevos flujos de electrones hacia abajo, abriéndose paso por el camino ionizado que dejó el líder escalonado. Estos son los líderes rápidos que al golpear tierra producen descargas de retorno menos energéticas que la primera. En un rayo es típico que existan tres o cuatro líderes, pueden existir hasta 20 ó 30.
El canal de la descarga en cuyo interior existe un hilo conductor de plasma, puede llegar a temperaturas de
30.000 ºC y la presión del aire subir hasta 100 atmósferas.
El diámetro del canal es de unos 10cm.
La descarga de una nube puede generar nuevas reparticiones de carga en la atmósfera, presentándose descargas horizontales entre varias nubes de tormenta. Es posible por lo tanto, que se desencadene otra descarga atmosférica de similar ubicación a la anterior, que utilice los mismos caminos ionizados que dejó la primera.
1.1.3 El trueno
“El trueno es la señal acústica generada por un canal de aire caliente que se expande rápidamente”, [6]. De él, se puede extraer información sobre la localización, tamaño y orientación del rayo.
Una teoría aceptada del trueno y sus principales rasgos, solo existe desde hace unos 25 años.
El aire en el canal de la descarga se calienta y se expande en forma de una onda de choque. Posteriormente, esta onda se vuelve energía acústica produciéndose el trueno. Cada componente del rayo: el líder escalonado, los líderes rápidos, las descargas de retorno, contribuyen al trueno.
Los componentes más energéticos producen las frecuencias más bajas del sonido. Estas frecuencias bajas se atenúan menos que las altas, ya que la atenuación es proporcional al cuadrado de la frecuencia. Por ello, un rayo no muy energético puede no oírse ya a 10 km.
El estudio del trueno ha perfeccionado los conocimientos que ya se tenían sobre el rayo y constituye un elemento fundamental para el estudio de las descargas entre las nubes y del canal de la descarga en el interior de una nube donde los medios visuales no pueden suministrar información. Adicionalmente, nos aporta criterios para la interpretación de los datos de nivel isoceráunico.
El nivel isoceráunico, número de días del año en los que se escuchan truenos, es actualmente el índice utilizado como indicativo de la cantidad de actividad eléctrica atmosférica de una región. De allí la importancia de entender las causas y características del trueno.
1.2 Características de la descarga eléctrica
Al impactar la descarga “de retorno” la línea de transmisión, produce corrientes altísimas que aumentan en unos pocos microsegundos. Se presentan corrientes pico entre 20 y 200 kA, aunque estas últimas son muy raras. La probabilidad de que se produzca una descarga mayor o igual a una determinada magnitud de corriente, se puede obtener de la figura 2. Aproximadamente el 90% de las descargas llevan carga negativa al sistema.
Para el comportamiento del sistema ente la descarga, es importante la rata de aumento de la corriente proveniente del rayo. Se suele suponer en los cálculos, que la corriente aumenta linealmente desde cero hasta el valor pico en forma de rampa, con un determinado tiempo de duración (tiempo de frente, ó de cresta), que se estabiliza un instante en el valor pico y luego decrece más lentamente hasta volver a cero.
Curvas típicas del porcentaje de rayos en función de la corriente de descarga:
A – De la AIEE
B – De Popolansky
C – De Anderson
La probabilidad de un determinado tiempo de frente de la descarga se observa en la figura 3.
Las características de corriente son diferentes cuando el objeto golpeado sobresale excesivamente del suelo. Así las mediciones hechas en el Empire State Building revelan valores de corriente diferentes a los mencionados, y aún mecanismos diferentes de la descarga. En estos casos el líder no sale de la nube sino del objeto alto.
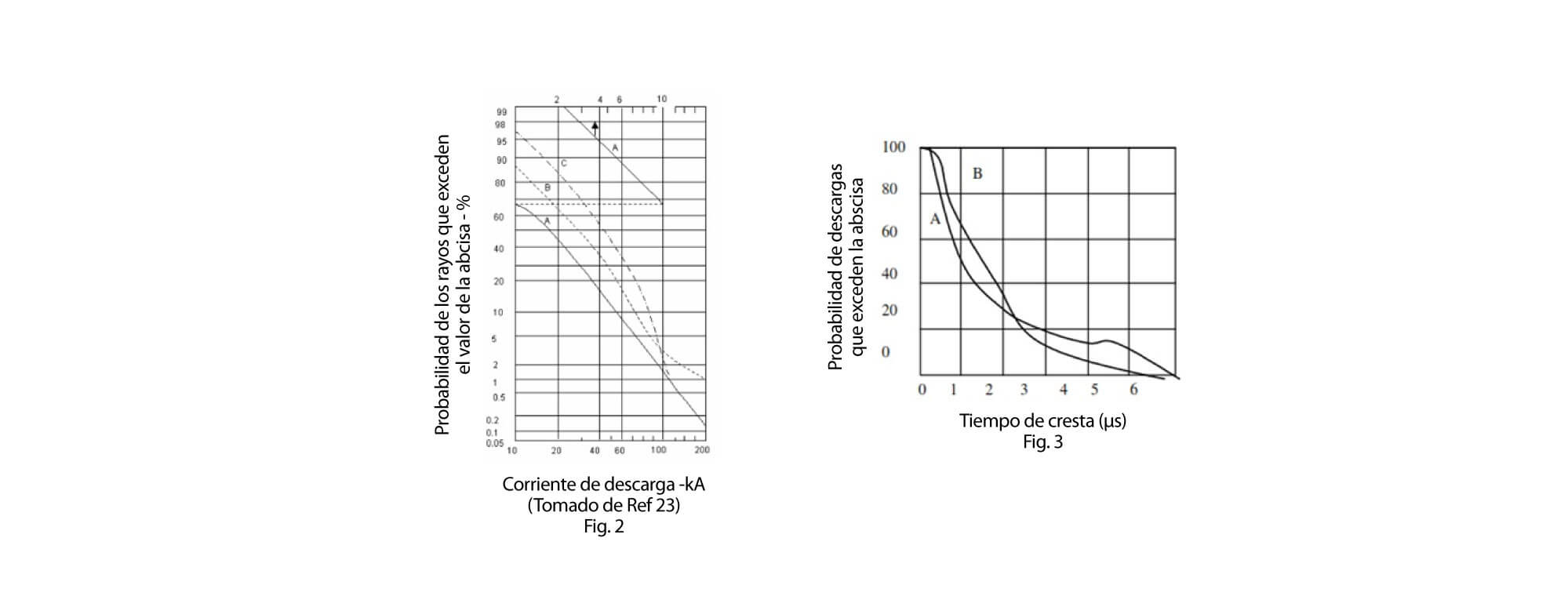
Distribución de tiempo de cresta en las descargas eléctricas:
A – De Mc Echaron
B – De Anderson
Para el valor de la corriente también se observa dependencia con respecto a la impedancia característica, tanto del sistema golpeado como del canal de la descarga (véase figura 4)
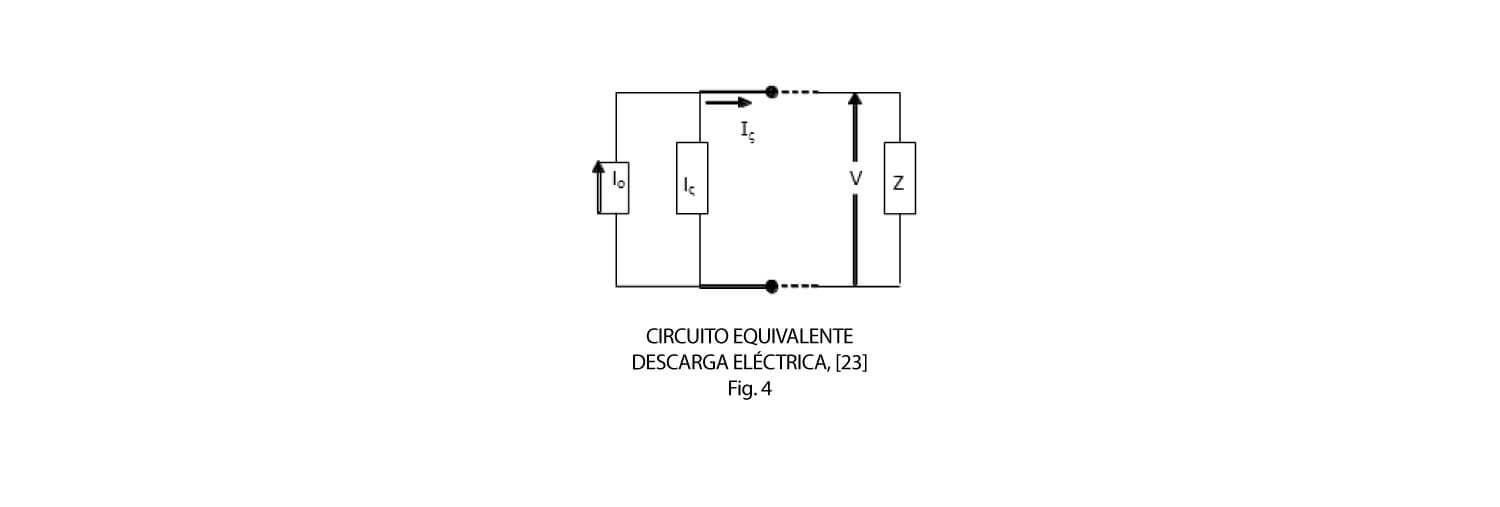
Io: Corriente de descarga prospectiva (fuente de corrienteconstante).
Iς: Corriente de descarga en la impedancia terminal (ZR).
Zς: Impedancia característica del canal de descarga.
ZR: Impedancia característica resultante.
V: Tensión sobre el objeto golpeado.
1.3 Medición de las descargas atmosféricas
Son incontables las herramientas que se han utilizado para medir las corrientes y voltajes de los rayos, desde los usados en 1910 y 1930 como el klidonógrafo, el oscilógrafo, la cámara de Boys, los medidores de corriente de cresta (magnetic links), hasta los sofisticados equipos utilizados por el proyecto francés del Massif Central de producción y medición de rayos “ artificiales”. Allí se emplean magnetic links, registradores de campo eléctrico y magnético cada uno con varios osciloscopios y equipo fotográfico integrado, goniómetro para localizar relámpagos; contadores CIGRE de relámpagos; medidores del campo de tierra (field mills and radioactive probe electrometer) y equipo fotográfico y acústico.
1.4 Nivel ceráunico
El nivel ceráunico está definido como el número de días del año en los cuales se escucha, por lo menos, un trueno en el lugar de observación.
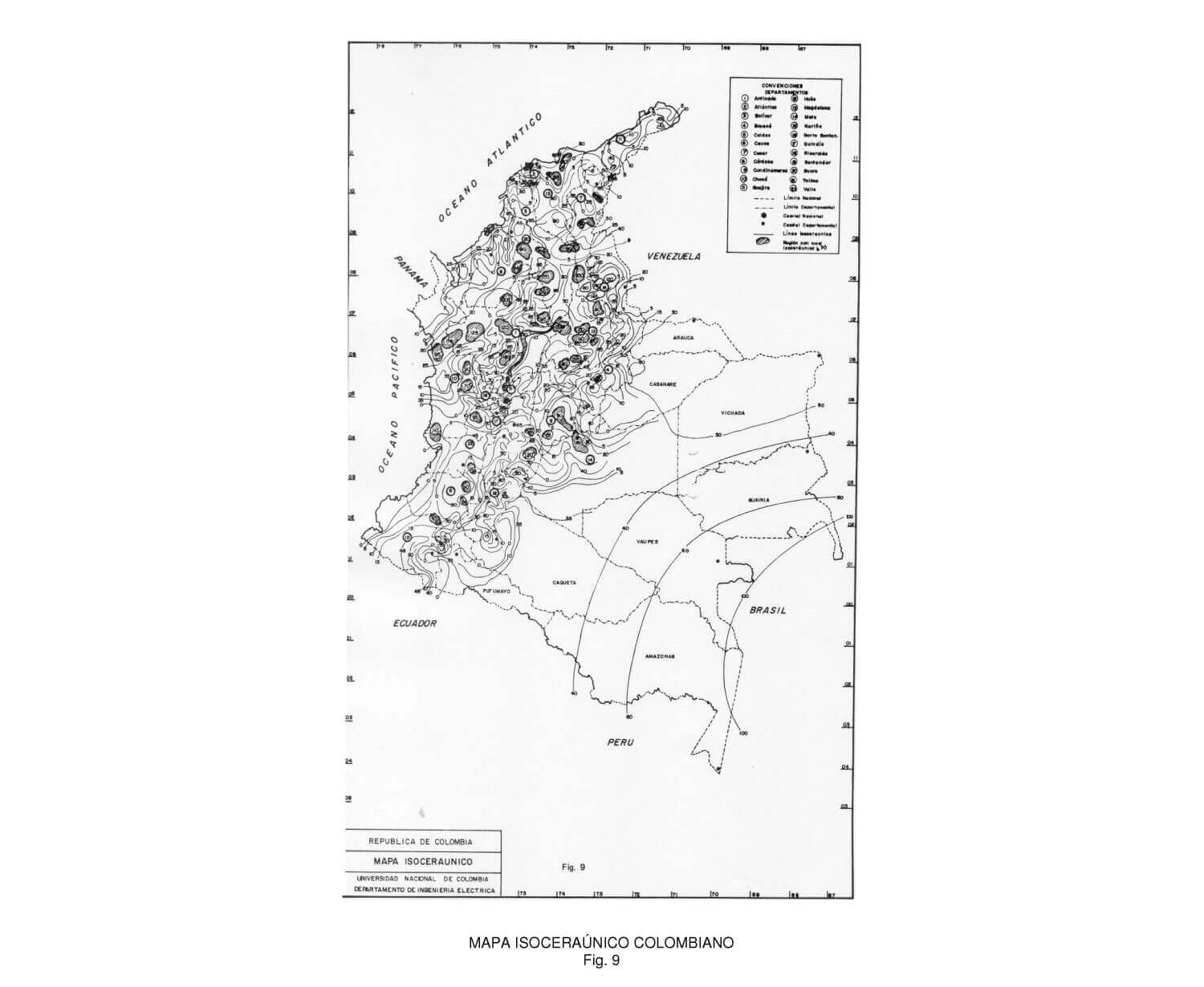
Los niveles ceráunicos se suelen llevar a mapas isoceráunicos, es decir, a mapas con curvas de igual nivel ceráunico.
La comparación del mapa isoceráunico de Colombia con el de Europa y aún el de EE.UU. Muestra la magnitud que este problema tiene para nosotros (figura 5 y figura 9).
2.0 Numero de descargas en una línea
El numero de descargas a una liena para un nivel isoceráunico dado, no es conocido actualmente con mucha certeza. El problema es de naturaleza estadística [7], por lo tanto los métodos aquí expuestos, en los cuales este número se encuentra determinísticamente, dan solo una aproximación al valor medio de la distribución.
Se parte de considerar una densidad de descargas (número de descargas / Km2) uniforme para una región con nivel ceráunico constante. A partir de esta densidad, se determina el número de esas descargas interceptado por la línea.
2.1 Densidad de descargas
El número de descargas por km cuadrado por año (N) ha sido estimado como proporcional al nivel isoceráunico.
N: K. (NI).
N: Número de descargas por Km2
NI: Nivel ceráunico.
K: Constante determinada con base en investigaciones de campo.

2.2 Sombra eléctrica
Se considera que la zona de influencia de una línea, llamada su sombra eléctrica (figura 6) o ancho de banda de atracción, depende de la altura del punto más alto de la línea sobre el terreno, que es el cable de guarda y de la distancia horizontal entre cables de guarda, si existe más de uno.
A = 4h + b
A: Ancho de la sombra eléctrica.
b: Distancia horizontal entre cables de guarda.
h: Altura efectiva sobre el terreno del cable de guarda.
La altura efectiva tiene en cuenta que la altura del cable varía desde hg en la torre, hasta hgv en la mitad del vano. Si el vano es plano:
h = hg − (hg – hgv ) * 2/3
Se debe tener en cuenta que no está cuantificada la influencia del paso de la línea por un terreno boscoso, el cual disminuye su altura efectiva, ni tampoco que la línea pueda estar en el borde de una montaña muy alta, lo que aumenta la posibilidad de la intercepción de los rayos.
2.3 Número de descargas directas a la línea
Es el producto de la densidad de descargas a la zona por la línea de influencia de ésta. Si queremos determinar el número de descargas a la línea por 100 km de longitud, NL, será entonces:
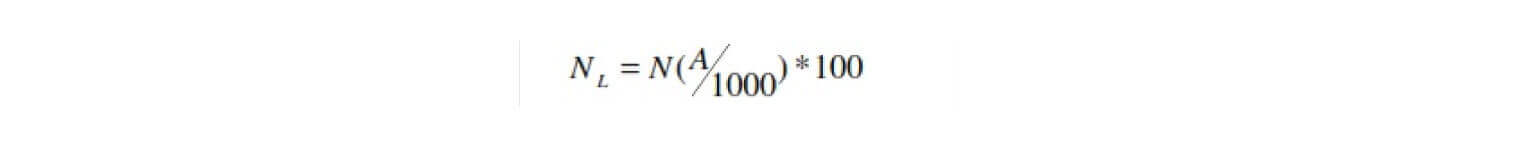
NL : Numero de descargas sobre la línea por 100 km por año.
N: Descarga por Km2 – año
A: Sombra Eléctrica en metros.
2.4 Distribución en torres y vanos
Si se ha hecho un buen cálculo del ángulo de apantallamiento del cable de guarda, de las descargas que alcanzan la línea, prácticamente ninguna golpeará el conductor, sino a la torre o al cable de guarda.
Las que golpean el cable de guarda en la mitad del vano, por lo general, no causan flameo por varias razones: El mecanismo de flameo entre conductores cilíndricos paralelos produce altísimas corrientes de pre-descarga, que rebajan el voltaje entre cable y fase, demorando un posible flameo; además, las reflexiones que llegan de las torres adyacentes, disminuyen aún más el voltaje; las distancias entre cable y fase son mucho mayores en el vano que en la torre.
Es importante, entonces, saber que porcentaje de las descargas totales golpea el cable de guarda lejos de la torre y cuantas descargas caen sobre la torre o el cable, en cercanías de esta.
J.G. Anderson [8] presenta para torres de acero con vanos de 300m un porcentaje de 60% de descargas a torre (o cerca). Para apoyos en madera el porcentaje es de un 25%.
Si el vano es mayor habrá menos torres, y por lo tanto menos descargas a torre por km. La ecuación que propone Anderson para el factor de reducción del número de descargas es:
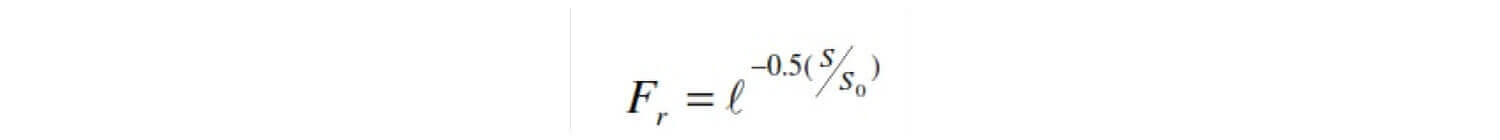
Fr: Fracción de descargas sobre el vano que caen directamente a la torre.
S: Vano usado en la línea.
S0: Vano base, en este caso 300m.
3.3. Salidas de la línea
Las salidas de las líneas se deben a muy diferentes razones. La empresa Interconexión Eléctrica S.A. (ISA), enumera siete diferentes causas que pueden observase en la tabla 1. Allí también encontramos las estadísticas de 1982 para las principales líneas a 220 kV. Podemos observar que la causa principal de salida son las descargas atmosféricas, es decir, los sobrevoltajes producidos por estas descargas.
Entre las salidas producidas por descargas atmosféricas se deben distinguir dos tipos: las salidas debidas a fallas de apantallamiento y las debidas a flameo inverso.
3.1 Salidas por fallas de apantallamiento
Estas salidas se deben a la caída de un rayo directamente sobre el conductor de fase, por falla del cable de guarda, encargado del apantallamiento de la línea.
Un rayo de 30kA, (que es muy probable, según la figura 1), produce en una línea con impedancia característica de 400 ohmios, ondas de voltaje a lado y lado del punto de impacto de 6000 kV, que exceden por amplio margen el BIL de una línea de 220kV (aproximadamente de 1050kV). Por esta razón la probabilidad de que haya flameo entre el conductor y la cruceta o entre dos fases adyacentes y se presente una posterior salida de la línea, es muy cercana al 100% si falla el apantallamiento.
Sin embargo, las fallas de apantallamiento en las líneas colombianas parecen ser bastante escasas debido a los pequeños ángulos de protección que se utilizan.
3.2 Salidas por flameo inverso
Cuando la descarga cae sobre el cable de guarda, viaja hasta la torre más cercana, (a cada lado del punto de impacto), donde busca su camino a tierra. Parte de la onda de choque se reflejará por el cable de guarda hacia atrás, parte se refractará por el cable hacia delante y la mayor parte, baja por la torre hacia tierra. Debido a la impedancia de la torre y a la resistencia de puesta a tierra, se forman a todo lo largo de aquella, voltajes de un valor bastante alto.
Cuando el voltaje ne la cruceta es muy alto con respecto al conductor, tenemos el flameo cuyo punto de mayor voltaje es la cruceta, llamado flameo inverso, (back flashover). Este flameo puede ocasionar, dependiendo del sistema de protecciones, una salida de la línea.
3.3 Número total de salidas de la línea por descargas atmosféricas
Sumando las salidas por falla de apantallamiento con las debidas al flameo inverso, se obtiene un número total de salidas debidas a descargas atmosféricas.
Este número debe ser menor o igual que un determinado valor de diseño, que deben determinar las compañías dueñas de la línea, de acuerdo con la mayor o menor repercusión que pueda tener una salida de la línea sobre el resto del sistema y sobre la carga que está alimentando.
4.4. Diseño del cable de guarda
El diseño de un cable de guarda consiste básicamente en la determinación de su ubicación en la estructura.
Las características mecánicas se deben considerar de tal forma, que resista la carga mecánica y no vaya a tener una flecha excesiva. Las características eléctricas, deben garantizar bajas pérdidas por inducción y bajos voltajes de paso y de contacto.
La ubicación del cable de guarda debe ser tal, que sea escasa la probabilidad de que caiga un rayo con una corriente suficiente para producir flameo.
Básicamente, se pueden dividir las metodologías de diseño de la ubicación del cable de guarda en dos grandes grupos: las que encuentran una posición “efectiva” del cable de guarda, tal que permita un “buen” apantallamiento y las que asignan a una posición determinada del cable de guarda, una cierta probabilidad de falla de apantallamiento.
4.1 Apantallamiento efectivo
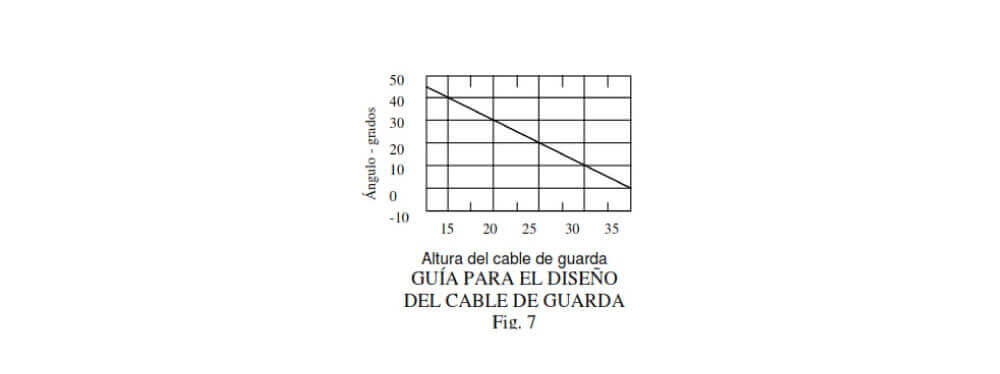
Existen metodologías más o menos sencillas para la ubicación de la posición efectiva. La más sencilla de todas, es mediante una gráfica como la de la figura 7, en la cual se encuentra la combinación de altura del cable con el ángulo de apantallamiento, los cuales producen un buen funcionamiento de líneas de Extra Alto Voltaje (EHV), [8].
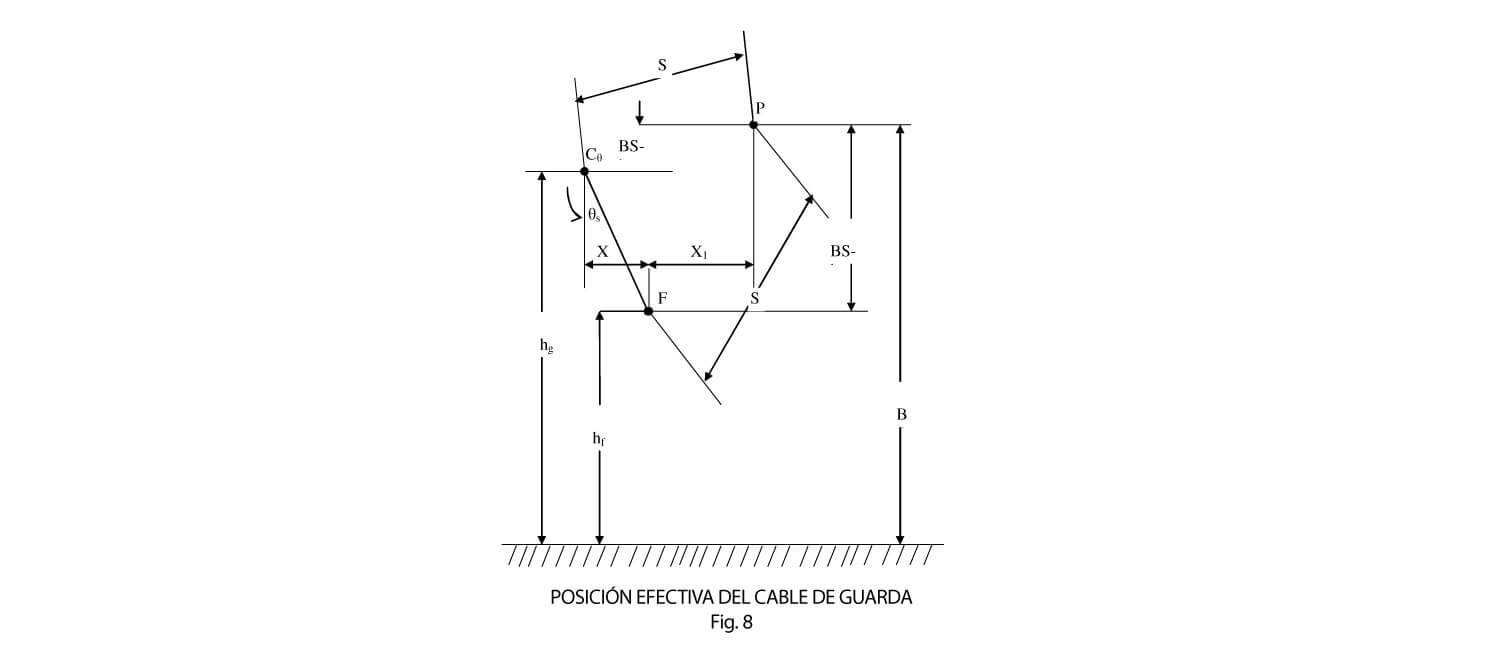
Una forma más elaborada, es mediante el modelo electro- geométrico. En la figura 8 se muestra la posición del cable de guarda, (Cg) del conductor (F) y del terreno. En el punto P se interceptan las áreas de atracción de estos tres elementos, de tal forma, que los rayos que caen a la izquierda de P son interceptados por el cable de guarda y los que caen a la derecha de P son atraídos a tierra.
El área de influencia del conductor y el cable de guarda, se extiende hasta una distancia S que se llama distancia de impacto. Para una altura de conductor determinada hf, se supone una altura del cable de guarda hg y para ella se encuentra el ángulo de apantallamiento θs y la distancia horizontal x, conductor y cable, según las siguientes fórmulas:
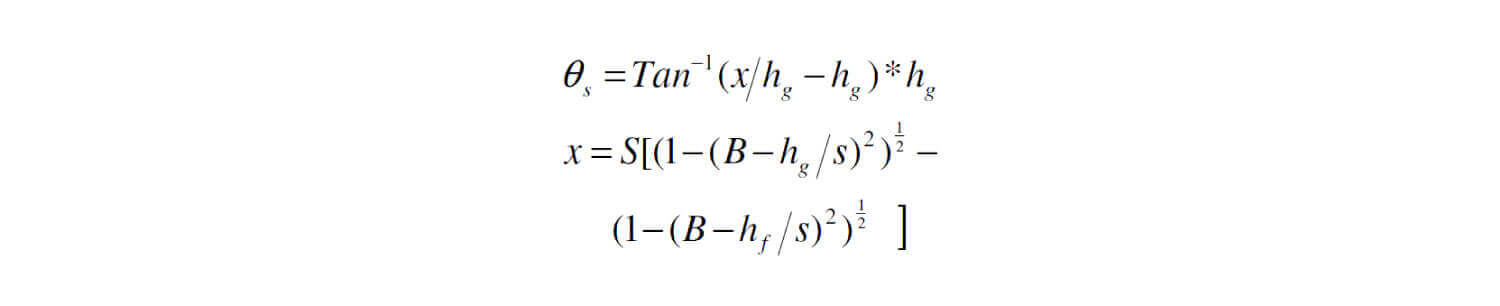
4.2 Distancia de impacto (s)
Si el líder escalonado se acerca hasta una distancia S del conductor o del cable de guarda, podrá vencer la rigidez dieléctrica del aire y golpear sobre el elemento en mención. Por eso, de lo que se trata, es que el rayo se acerque primero al cable de guarda o a tierra, antes que al conductor. Esta distancia de impacto es mayor mientras la carga que ha descendido hasta la punta del líder sea mayor. Esta carga es la que produce una mayor o menor corriente en el rayo. Existen varias fórmulas empíricas basadas en diferentes mediciones. En [8] se presenta la siguiente expresión:
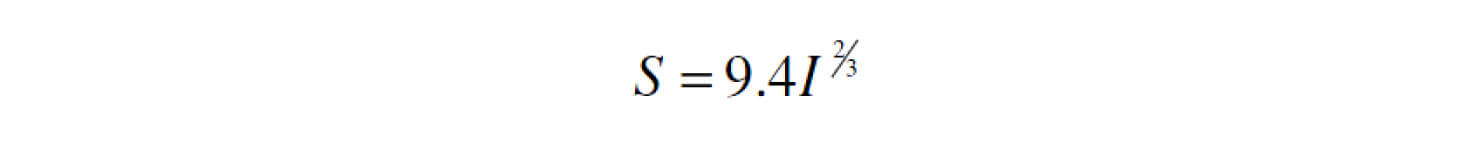
S: Distancia de impacto en metros
I: Corriente de rayo en KA
El conductor debe ser protegido de corrientes mayores o iguales a Ic. Siendo Ic la corriente de la descarga que al caer sobre el cable de guarda producirá un voltaje igual al BIL de la cadena de aisladores. De tal forma que para el apantallamiento efectivo la distancia de impacto S se calcula con base en la corriente crítica Ic:
Ic = 2 BIL/Z0
BIL: Nivel básico de aislamiento de la cadena de aisladores, kV.
Z0: Impedancia característica en ohmios.
La impedancia de un conductor con retorno por tierra y de resistencia cero, despreciando resistencia y conductancia será:
Z 0 = 60Ln (2h / r)
h: Altura del conductor en metros.
r: Radio del conductor en metros.
4.3 Probabilidad de falla del apantallamiento
Existen varios métodos cuyo resultado de una determinada posición del cable de guarda, define una probabilidad de falla de apantallamiento.
El más directo de estos métodos es el que se basa en la Ecuación de Burgsdorf-Kostenko:
Log (Pθ ) = θs h2/2 * 90 – 2
θs Angulo de apantallamiento, grados.
Pθ Probabilidad de falla del apantallamiento (%).
H: Altura de cable de guarda, metros.
Para encontrar el número de fallas por apantallamiento, se multiplica Pᶱ /100 km por el número de descargas directas a la línea, por 100 Km de longitud y por año (NL).
De acuerdo con experiencias de campo en Rusia, aplicables a torres entre 25 y 30m de altura teniendo en cuenta la altura promedio ( h ) del cable de guarda, tenemos otra expresión equivalente para NL
NL = 2.7 h (NI) / 30 descargas/100 km-año
Es apropiado, entonces, acoplar Pθ y NL. Solamente una porción de fallas por apantallamiento producirá flameos. La magnitud de corriente crítica de descarga que produce flameo es:
I c = 2v Z 0
Donde
V: Voltaje de flameo crítico del aislamiento de la torre.
Zo: Impedancia característica del conductor.
Burgsdorf, también proporciona una fórmula empírica para la probabilidad (P1 0/0) en que una descarga excederá el valor (I, kA):
Log (P1) = 2 – I /60
La expresión anterior daría una curva similar a la presentada en la figura 2.
La rata de flameo por apantallamiento está dada por:
SFO = NL P1 P� 10-4
Métodos más refinados tienen en cuenta la probabilidad existente de que un rayo caiga haciendo un determinado ángulo con la vertical, la probabilidad de que caiga un rayo de una determinada magnitud, el BIL del aislamiento, etc.
Un método tal es el desarrollado por Whitehead y Brown, [11]
5. Fallas del aislamiento por flameo inverso
Ya se explicó en el numeral 4.2 cuál es la causa del flameo inverso, es necesario conocer el voltaje que se presenta entre la cruceta y el conductor, debido a la descarga que baja por la torre a tierra, además, es necesario determinar la probabilidad de que se produzcan corrientes de la magnitud de las que pueden producir flameo.
5.1 Cálculo del voltaje a través del aislamiento
Se han utilizado diferentes metodologías para conocer esos voltajes, estas técnicas básicamente pueden ser análogas o digitales.
La técnica análoga más utilizada, es la de construir un modelo geométrico de la torre con cada uno de sus componentes, [12], se inyecta momentáneamente una gran corriente por medio de un cable colocado verticalmente sobre la torre, simulando el canal de la descarga. Se producen en ese momento campos eléctricos y magnéticos similares a los presentes en la línea cuando cae un rayo.
Mediante la medición directa del voltaje entre la cruceta y el conductor y utilizando escalas, se conoce el voltaje real que se presentaría en la línea. La escala es tal, que si, por ejemplo, se reducen las dimensiones de la torre en 25 veces, la frecuencia debe aumentar en esas 25 veces. Esto significa que en el modelo se deben realizar medidas a muy altas frecuencias y en tiempos muy reducidos.
Otras técnicas análogas usadas en el análisis transitorio de sistemas de potencia como el TNA, no son usadas en este caso ya que no simulan el comportamiento variable de los campos electromagnéticos en la complicada geometría de la torre.
Las técnicas digitales que se utilizan, son procedimientos que deducen analíticamente el valor del voltaje a partir del valor de la corriente, de su tiempo de frente de ondas y su forma. Parten de la teoría de campos electromagnéticos o directamente de la teoría de circuitos, bien sea de parámetros concentrados o distribuidos.
Partiendo de las ecuaciones de Maxwell, se pueden desarrollar fórmulas para el voltaje con base en la corriente, utilizando los métodos de lazo de potencial o de cancelación de campo, [13], [14] y [15]. En estos casos para simplificar la complejidad de la geometría, se suele reducir la línea a cilindros o conos equivalentes.
Se puede partir directamente de la teoría de circuitos, en cuyo caso, se debe considerar que cualquier fenómeno transitorio es una “mezcla de efectos de las ondas viajeras (en cables y líneas) y de oscilaciones de circuitos de parámetros concentrados (generadores, transformadores, tierras, etc.)”, [16].
Los problemas de ondas viajeras se pueden resolver mediante las técnicas de Bewley (lattice) o de Bergeron (características), utilizando además técnicas adicionales para la consideración de los parámetros concentrados.
Se han intentado también, algunas simplificaciones en el tratamiento de estos fenómenos transitorios:
a. El método de la AIEE, [17], considera la torre en serie con su resistencia de puesta a tierra como un circuito RL serie. El valor de referencia para la inductancia de la torre fue de 20µH. Considera además la variación de la impedancia de los contrapesos en el tiempo, debido a la impedancia característica del contrapeso de alrededor de 150 ohmios que evoluciona hasta su valor en DC. Este método fue revaluado a partir de experiencias con líneas de voltaje a 220 kV y superiore
b. El método utilizado por J.G. Anderson para líneas de más de 345 kV, [8], desprecia prácticamente la inductancia y se concentra simplemente en el efecto de la resistencia de puesta a tierra. Esta aproximación es factible debido a que el voltaje producido por el cambio de campo magnético en la torre, es menor que BIL de las líneas a esos niveles de voltaje.
El método aquí presentado es diferente de los anteriores; considera la torre como una impedancia característica y mediante el análisis de las reflexiones de la onda viajera, determina el voltaje a través del aislamiento.
5.2 Ondas viajeras
Cuando la frecuencia de una señal electromagnética que viaja por una línea es muy grande o, lo que es similar, cuando su duración es muy corta, se deben analizar en detalle la transmisión de la perturbación de los campos electromagnéticos a través del tiempo, mediante un análisis de la onda viajera.
V = IZ,
Siendo:
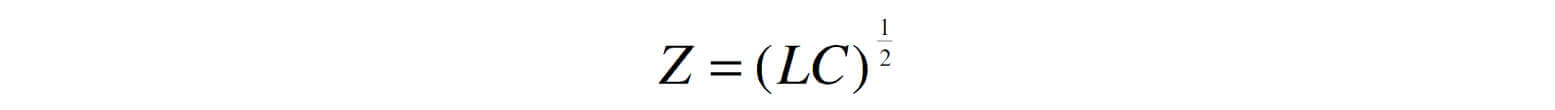
La fórmula para la impedancia característica de un conductor despreciando R y G ya se dio en el numeral 5.2.
Cuando una onda viajera pasa de un medio con impedancia característica Z1 a otro de impedancia Z2, se producen ondas de voltaje y corriente reflejadas y refractadas.
Los coeficientes de reflexión B y de refracción A tienen las siguientes expresiones:
B = (Z 2 − Z1 ) / (Z1 + Z 2 )
A = 2Z 2) /(Z1 + Z 2 )
El coeficiente de reflexión del voltaje en la base de la torre sería Bbt:
Bbt = (R – Zt ) / (R + Zt )
Zt: Impedancia característica de la torre.
R: Resistencia de la puesta a tierra.
Como se puede ver en la ecuación, el coeficiente de reflexión puede ser positivo o negativo. Si es negativo, la onda reflejada va a restarse al voltaje que está subiendo a medida que sube la corriente de la descarga hasta su valor máximo; por lo tanto, una reflexión negativa reduce el riesgo de flameo inverso. Inversamente, el peligro de flameo aumenta considerablemente si Bbt es positivo, es decir, si el valor d la puesta a tierra es superior al de la impedancia de la torre.
5.3 Impedancia característica de una torre
Este valor se determina por lo general, de modelos a escala de la torre. Debido a su complicada geometría el cálculo analítico es complejo.
Sin embargo, con base en medidas de este tipo y análisis teóricos, se han elaborado fórmulas que tienen buena coincidencia con los datos medidos. La fórmula más utilizada es la de Jordan:
Z t = 60 * ln(h r) + 90(r h) − 60
Zt: Impedancia característica de la torre en ohmios.
h: Altura total de la torre en metros.
r: Radio equivalente para diferentes tipos de torres utilizadas en Colombia calculadas de acuerdo con la ref. 8.
La impedancia de las torres usadas en líneas de 230 kV da entre 50 y 250 ohmios, siendo mayor mientras más esbelta sea la torre.
5.4 Impedancia de la puesta a tierra
La puesta a tierra se comporta de modo variable con el tiempo, ya que en los primeros instantes es muy importante el valor de la impedancia característica de los contrapesos y las varillas de puesta a tierra.
Si los contrapesos son muy extensos, este tiempo es muy largo y aumenta la probabilidad de flameo, ya que la impedancia de los contrapesos tiene valores que oscilan alrededor de 150 ohmios.
6. Cálculo de salidas por descarga atmosféricas
Una vez establecido el comportamiento de la torre ante descargas, se debe establecer la probabilidad de salida de línea, debido a las descargas atmosféricas. Como ya se aclaró, si el diseño del cable de guarda es apropiado, prácticamente todas las salidas de la línea se deberán a flameo inverso.
Para una línea de torres y vanos iguales se debe establecer la probabilidad del impacto de un rayo de determinada magnitud, con determinado tiempo de frente de onda que caiga en cierta parte del vano o en la torre.
Además, si se quiere evaluar el comportamiento de una línea real se debe considerar la particularidad de cada uno de sus vanos y torres.
6.1 variables probabilísticas de una torre
Para determinar en una torre el número de salidas por flameo inverso, se parte del número de descargas a la torre, (o de una curva de distribución de probabilidad de frecuencias), de la distribución de probabilidad de la magnitud de la corriente, de las distribuciones de frecuencia de los tiempos de frente de onda y de la localización de la descarga.
Adicionalmente, se pueden considerar las variaciones de la puesta a tierra, del voltaje de 60 ciclos, de las características dieléctricas del aislamiento y de otras condiciones variables.
Se han elaborado diferentes metodologías para con base en esos datos, establecer el número de salidas.
El método de Montecarlo, [19], por ejemplo, ejecuta una simulación estadística mediante la generación de números aleatorios para las diferentes distribuciones de probabilidad. Se generan miles de casos, en cada uno de los cuales se determina el voltaje de flameo inverso y se establece si hay o no flameo. Luego, establece el número de salidas sobre el total de eventos y por tanto la probabilidad de salida.
Otro método similar, el método estocástico de Sato, [20], en vez de generar valores aleatorios, divide cada distribución en intervalos y hace todas las combinaciones posibles entre estos intervalos. Para cada combinación de intervalos se establece la probabilidad de salida. Luego se suman todas las probabilidades de salida para obtener la probabilidad total.
6.2 variaciones a lo largo de la línea
Es bastante aleccionador el tomar una línea real y analizar torre por torre sus particularidades.
Un análisis de este tipo se realizó en un proyecto de grado dirigido por el autor, [21], en el cual se estudió la línea Paipa-Bucaramanga con todas sus particularidades. Para cada torre se estudió su comportamiento ante las descargas atmosféricas por medio de ondas viajeras. Se estableció que unas torres presentan comportamientos especialmente críticos. Por ejemplo, la torre No 28 tipo amarre CB, ubicada en el trayecto Paipa-Bucaramanga, presenta 1/14 de todas las salidas de la línea compuesta por 341 torres. En solo 18 torres de las 341 (5%) estarían el 41% de las salidas de la línea.
Este comportamiento se debe básicamente a los valores de resistencia de puesta a tierra que, por ejemplo, para las torres número 28 fue 50 ohmios. Esto se combina con el hecho de estar la torre en la zona de mayor nivel isoceráunico (65). También influye la geometría de las torres, ya que, a mayor altura, estas atraen más rayos y además el tiempo que demora en llegar reflexión puede ser considerable permitiendo un mayor pico de voltaje resultante.
Una torre alta y ancha presenta peor comportamiento, debido a que adicionalmente, si es muy ancha su impedancia característica es menor, y por lo tanto la reflexión puede tener un valor absoluto muy pequeño o, lo que es peor, puede llegar a ser positiva.
Esta situación lleva a una concentración del problema de las descargas atmosféricas que puede llegar a convertir unas pocas torres, en las potencialmente más peligrosas para la obtención del flameo inverso. Esta consideración se puede complementar con los datos sobre mayor actividad atmosférica observada en determinados relieves del terreno; con el conocimiento de torres localizadas en los bordes de las montañas o sitios igualmente expuestos, con la existencia de resistencias de puesta a tierra altas, de tal forma que se puedan tomar las medidas correctivas del caso tales como la mejora de la resistencia o el sobreaislamiento.
6.3 determinación gráfica del número de salidas
Debido a lo elaborado de los cálculos de salidas por flameo inverso, es usual utilizar gráficas de rápido manejo como las que se presentan en [17] y [22], de amplio uso en el país.
En las figuras 10 11 y 12 tomadas de [21], se presenta un método elaborado con base en las torres de la línea Paipa- Bucaramanga, para encontrar el número “n” de salidas por flameo inverso.
Para hallar el número de salidas de la línea se procede de la siguiente manera:
1. De acuerdo con la figura 9, con el valor de la resistencia de la puesta a tierra y el número de aisladores, se encuentra la tensión en el tope de la torre producida por el rayo y necesaria para que haya flameo.
2. De acuerdo con la figura 10, se encuentra la corriente crítica Ic, con base en el voltaje en el tope de la torre y el tipo de la misma.
3. Con Ic, encontramos en la figura 2, P(Ic), que era otro dato necesario para hallar “n” en la figura 11.
7. Conclusiones
En conclusión podríamos anotar, que, en el país, con niveles isoceráunicos tan altos, con un sistema interconectado a 230 kV en crecimiento y muy sensible a los sobrevoltajes por descargas atmosféricas, se deben llevar registros muy buenos de las salidas de las líneas, de las resistencias de puesta a tierra, de los datos geométricos de las líneas. Además, se deben estudiar los casos particulares más críticos y realizar investigaciones que permitan dar soluciones más apropiadas y económicas.
Bibliogrfía
(1) LARSON, ALEX. “Photographing lightning with a moving camera”. Annual report Smithsonian Institute, 1905.
(2) “Investigations on lightning discharges and on the electrical field of thunderstorms”. C.T.R. Wilson, Philosophical Tr., Royal Society, 1920.
(3) PETERS, J.F. “The Klydonograph”. Electrical world, abril, 1924.
(4) LEE, E.S. “Cathode ray oscillographs and their uses”. General Electric review, Vol. 31, 1928.
(5) BELL, E. Y A. PRICE. “Lightining investigations on the 220 kV system of Pennsylvania power and light Co.” (1930). AIEE Tr. Vol. 50-1931.
(6) FEW, ARTHUR A. “Thunder”. Scientific American. (7) “EHV Transmission line reference book”. Edison Electric Inst. New York, 1968.
(8) “Transmission lines reference book 345 kV and above”, EPRI, 1975.
(9) CHAMBERS, F. “Performance of 161 kV and 115 kV transmission lines”. AIEE, Oct. 1962.
(10) WHITEHEAD, GILMAN. “The mechanism of lightning flashover on HV and EHV lines”. Electra, March, 1973.
(11) BROWN, G.G. y E.R. WHITEHEAD. “Field and analytical studies on transmission line shielding”. IEEE-PAS, Vol. 88-1969.
(12) HAGENGUTH, J.H. et al. “Determination of lightning response of transmission lines by means of geometrical models”. AIEE Tr. Feb, 1960.
(13) WAGNER, C.F. y A.R. HILEMAN. “The lightning stroke”. AIEE Tr. Junio 1958.
(14) WAGNER, C.F. y A.R. HILEMAN. “A new approach to the calculation of lightning performance of lines: Pt III”. Tr. Oct. 1960.
(15) WAGNER, C.F. y A.R. HILEMAN. “A new approach to the calculation of lightning performance of lines: Pt II”. Dec. 1959.
(16) DOMMEL, H.W. y W. SCOTT MEYER. “Computation of electromagnetic transients “. IEEE-PAS. Jul 1974.
(17) “A method of estimating lightning performance of transmission lines”. AIEE COMITÉ REPORT – Tr. Vol. 69, 1950.
(18) CANO, F.I. y otros. “Determinación de las curvas de salida de las líneas de transmisión Colombianas debido a descargas atmosféricas”. Proyecto de grado U. Nacional. 1981. Director: Ing. Guillermo Rodríguez.
(19) ANDERSON, J.G. “Montecarlo computer calculation of transmission line lightning performance”. AIEE Tr. Ago 1961.
(20) SATO, A. “Estimating transmission line lightning outages by stochastic calculations”. IEEE-PAS. May- Jun 1980.
(21) ARTEAGA, G. y otros. “Estudio analítico y estadístico del comportamiento ante descargas atmosféricas de líneas de transmisión a 220 kV en Colombia”. Proyecto de grado U. Nacional. Director: Ing. Antonio Mejía Umaña. 1982
(22) CAYTON, J.M. y E.S. YOUNG. “Estimating lightning performance of lines”. IEEE-PAS. Nov. 1964.
(23) CASTILLO, G. y otros. “Metodología de diseño de aislamiento por descargas atmosféricas en líneas de transmisión”. Proyecto de grado U. Nacional, 1981. Director: Ing. Antonio Mejía Umaña.