Resumen: En el presente trabajo se hace una breve descripción de las labores desarrolladas por los autores durante los años de 1985 y 1986 y ubicadas dentro de las actividades dirigidas al estudio del campo electromagnético adelantadas por el grupo de investigación en Alta Tensión “GIAT” del departamento de Ingeniería Eléctrica de la Universidad Nacional. En ellas se demostró el comportamiento no lineal de la distribución de voltaje en las cadenas de aisladores empleando diferentes métodos, entre los cuales se pueden enumerar los métodos computacionales de las capacidades equivalentes y de las diferencias finitas y varios métodos experimentales. Las comparaciones de resultados teórico- computacionales y experimentales arrojaron resultados muy satisfactorios.
Introducción
En el diseño del aislamiento en sistemas de alta tensión, tanto por razones de economía como de seguridad, es necesario conocer la distribución del campo eléctrico y del potencial en el elemento dominante, cosa que ha tomado vital importancia con la tendencia y la necesidad actual de utilizar cada vez mayores tensiones en la transmisión de energía. Se observará que la distribución de potencial y de campo eléctrico en una cadena de aisladores no es lineal, esto quiere decir que cada aislador o unidad está sometida a un valor diferente de tensión, dependiendo de su ubicación en la mencionada cadena, presentándose los mayores gradientes en las unidades más cercanas a la línea.
Un aislador puede representarse eléctricamente por un condensador formado a su vez por otros en serie y cuyos dieléctricos son la porcelana o el vidrio. Tal condensador es imperfecto, y la corriente que lo atraviesa tiene una componente activa (en fase con la tensión) debido a varios tipos de pérdidas y otra componente en cuadratura con la anterior, producida por la capacidad. Cuando los aisladores se encuentran a la intemperie, por efectos de la contaminación, la superficie conductora aumenta y con esta la capacidad, aumentando de manera simultánea la corriente de pérdidas por la reducción de la distancia de flameo, resultando así una disminución en la tensión de formación del arco, en comparación con la de un aislador limpio y seco.
1. Circuito equivalente
En una cadena de aisladores se manifiestan varios grupos de capacidades asociadas a las diferentes partes que la constituyen; tales son:
1. La capacidad debida al dieléctrico (porcelana o vidrio), entre la cuenca y el pin de cada unidad (C).
2. La capacidad entre las partes metálicas (herrajes) y el terminal de tierra (torre), debida principalmente al dieléctrico aire, siendo capacidades de dispersión (Ce).
3. La capacidad entre cualquier elemento metálico de la cadena y todos los demás elementos metálicos de la misma (Cpm).
4. La capacidad entre las partes metálicas (herrajes) y el conductor de fase (K).
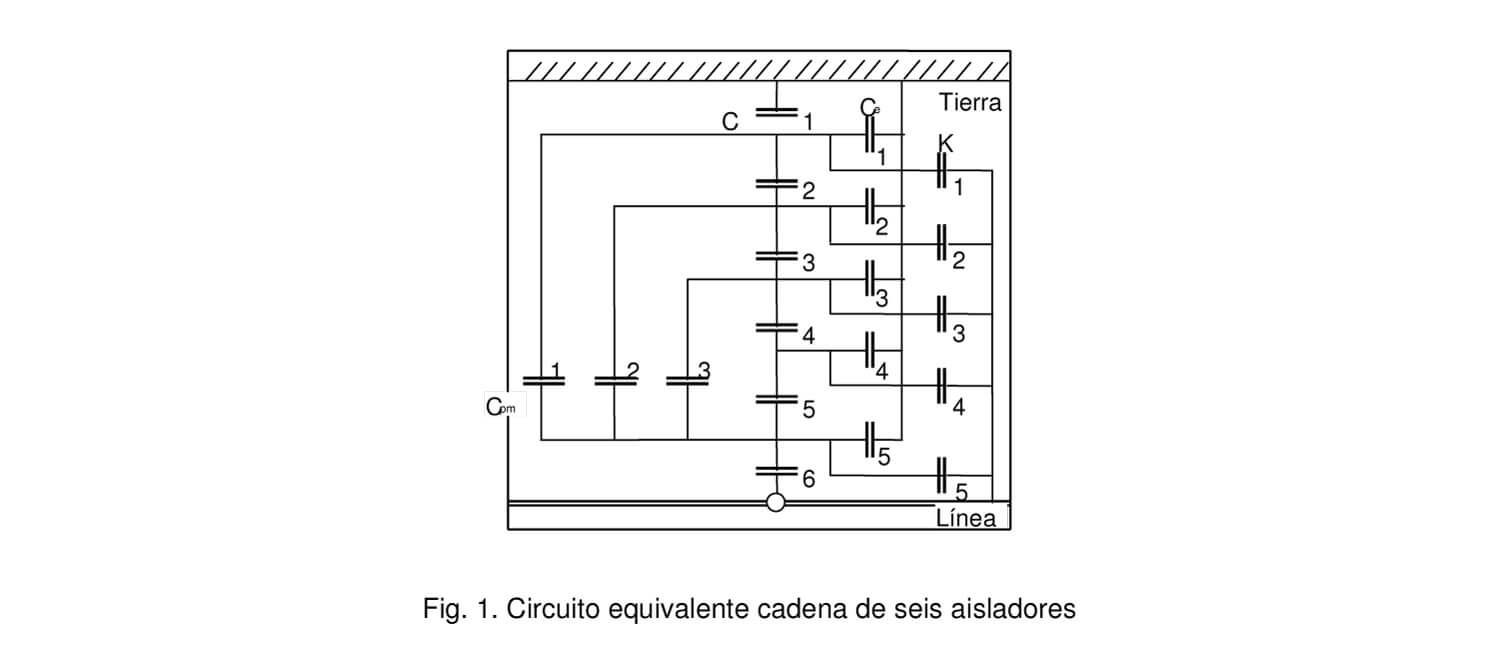
La figura 1 muestra estos cuatro grupos de capacidades para una cadena de aisladores. Nótese que para la capacidad entre partes metálicas Cpm, por simplicidad del dibujo, solo se representan las referidas a un aislador. En general para una cadena de N aisladores se tienen NxN capacidades involucradas.
La determinación exacta de Cpm es muy compleja y su efecto aunque notorio no es de los más significativos, por lo tanto puede despreciarse en muchos casos /5/. Según las mediciones la capacidad K es muy pequeña comparada con Ce siendo siempre menor del 10% /1/, con lo cual, al despreciarla, se simplifica mucho el circuito equivalente.
2.Método computacional de las capacidades equivalentes
Este es un método matemático que toma como base el circuito equivalente y mediante sucesivas reducciones serie-paralelo y estrella-triángulo obtiene el circuito mínimo, su tensión y su corriente, luego se regresa por el mismo proceso, de unidad en unidad, determinando la capacidad equivalente de cada aislador, el porcentaje del voltaje que soporta, la caída de tensión individual y acumulada, la corriente por cada unidad y las pérdidas de potencia aparente por la cadena. Al final se obtiene que la fórmula general para el cálculo de los potenciales es:
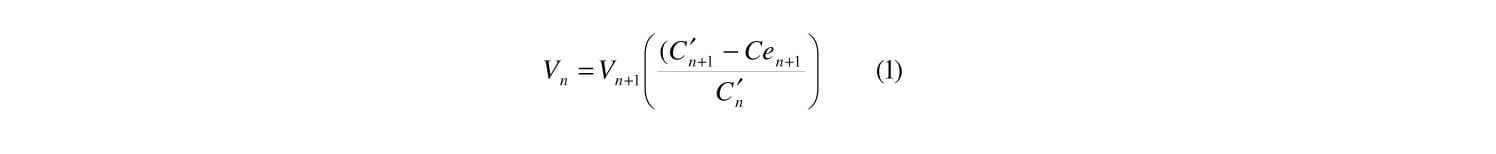
Vn: Tensión acumulada en el n-ésimo aislador
Cn: Capacidad equivalente desde el mismo aislador
Ce: Capacidad a tierra desde el aislador
Sin entrar en detalles matemáticos ni cuantitativos la interpretación de resultados del programa de computador, proporcionó las siguientes conclusiones:
1.Al aumentar la capacidad entre cuenca y pin (C) la distribución de potencial se hace más lineal, sin embargo es aún muy notoria la diferencia entre el voltaje soportado por las primeras unidades de la cadena y las últimas.
2.Al aumentar la capacidad de cada unidad a tierra (Ce) la distribución se hace menos lineal, esto es de esperarse puesto que son éstas capacidades parásitas las que producen esta no-linealidad.
3.En términos generales puede decirse que la distribución de potencial es independiente de la magnitud de la tensión aplicada, es decir se obtienen los mismos porcentajes de tensión para cada aislador. Sin embargo, a medida que estos son más sobrecargados por efecto del campo eléctrico, aumentan los fenómenos tales como el efecto corona, que varían totalmente el modelo ya que aparecen nuevos elementos en el circuito equivalente.
4.Las variaciones en baja frecuencia no afectan la distribución de potencial en la cadena, sin embargo, a muy altas frecuencias aparecen fenómenos diferentes asociados a la disrupción en el aire y comportamiento de los aisladores.
5.Al aumentar el número de aisladores en la cadena se aumenta el efecto de la no-linealidad, es decir, aumentan las diferencias entre las primeras unidades y las últimas. A manera de ejemplo en una cadena de tres aisladores los porcentajes obtenidos son: 29.3, 32.3 y 38.4% respectivamente, mientras en 30 aisladores al primero le corresponden 0.005% y al
último 27.0%.
3.Método numérico de las diferencias finitas
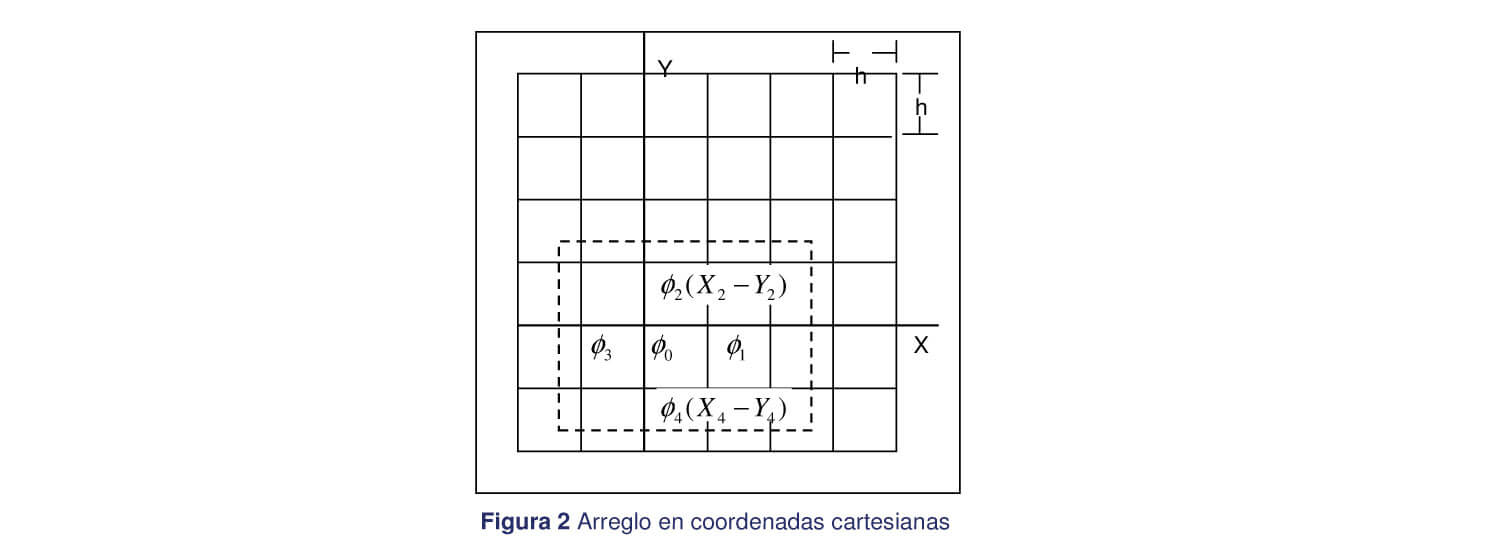
El método de las diferencias finitas se basa en el uso de la ecuación diferencial de Laplace expandida en una serie de Taylor. El potencial en un punto determinado se calcula de acuerdo con los potenciales conocidos de puntos vecinos a el; para lo cual se debe elaborar un sistema de red, que generalmente es de forma cuadrada, pero que también puede ser triangular o hexagonal.
Teniendo en cuenta un campo eléctrico de dos dimensiones, los términos hasta de segundo orden en la serie de Taylor (para un cierto grado de exactitud), una red de forma cuadrada de ancho h y suponiendo que el potencial en el punto (X0,Y0) se encuentra localizado en el origen de coordenadas; se obtiene el potencial en el punto 0, en función de los cuatro puntos, por aplicación de la ecuación diferencial de Laplace sobre cada uno. En la figura 2 se aprecia este tipo de arreglo.
Dado que el aislador presenta en su configuración cambios de dieléctrico, estos se tienen en cuenta para ser introducidos en el programa, así como también un factor de aceleración para una rápida convergencia en el proceso iterativo /2/. El programa desarrollado puede ser empleado para cualquier configuración de electrodos empleando para ello un tiempo de cálculo razonable.
Este método, como todos los de geometría abierta implica el conocimiento previo de las condiciones de frontera, las cuales son normalmente asumidas y no se puede asegurar su exactitud, por lo tanto se tomaron inicialmente matrices muy grandes, en las cuales el tamaño del objeto en estudio fuera despreciable y con condiciones de frontera nulas. Posteriormente se hacen ampliaciones graduales de ese objeto pero con condiciones de frontera más reales tomadas de la ampliación anterior, hasta obtener detalles del campo eléctrico en el interior del objeto estudiado. El método fue utilizado para encontrar las líneas equipotenciales y con ellas la tensión soportada en las diferentes partes de un aislador tipo pin de alto voltaje, un aislador de suspensión y una cadena con tres de estos aisladores /2/. Las líneas de campo eléctrico son perpendiculares a las equipotenciales y su magnitud es inversamente proporcional a la distancia entre estas.
AISLADOR TIPO PIN
Para este aislador se logró visualizar la configuración de las líneas equipotenciales a través de la porcelana y sobre su superficie, obteniéndose la mayor concentración de campo eléctrico entre el pin y el conductor, como puede apreciarse en la figura 3. Análogamente se estudió el aislador llamado de radio-interferencia con resultados diferentes debido a su recubrimiento especial.
AISLADOR DE SUSPENSIÓN
Se elaboró un estudio similar al anterior para este tipo de aislador y las líneas equipotenciales así obtenidas pueden apreciase en la figura 4, destacándose las zonas donde se concentra el campo eléctrico, que corresponde al sitio de mayor concentración de las líneas equipotenciales.
CADENA DE TRES AISLADORES
El método seguido es similar al de los aisladores de pin y de suspensión y las líneas equipotenciales obtenidas pueden apreciarse en la figura 5.
